Appendix 2 - Mathematical requirements
|
Mathematics, the bane of many students lives! Apart from the four rules of number (addition, subtraction, multiplication and division) there are other mathematical techniques and concepts that are essential at this level. Paper 1 (HL and SL) does not allow calculators and so any calculations use simple numerical relationships. Ensure that you are familiar with all of the concepts below.
|
Calculations and basic arithmetic functions - the four rules of number
The four rules of number are addition, subtraction, multiplication and division. In paper 1 no calculators are allowed, so the basic maths requirement is simple manipulation of these rules.
For instance, you will be expected to be able to divide and multiply by 2, but not by 1.3 (unless the number you are dividing is clearly a multiple of 1.3, eg 4.6)
Manipulation of equations is something that some students get confused with.
Subtraction and addition
Whatever operation is done to the left hand side MUST be done to the right hand side. In other words, if something (a number or a symbol) is subtracted from the left hand side it must also be subtracted from the right hand side. Add to the left and we must also add to the right.
|
Example: For the equation: A + B = C + D If we subtract 'A' from the left it must also be subtracted from the right for the equation to remain correct A + B - A = C + D - A Which cancels down to: B = C + D - A We have taken a term (in this case 'A') from the left to the right CHANGING THE SIGN as we did so. This is an allowed mathematical manipulation. |
Multiplication and division
Take the equation:
| A | x | B | = | R | x | S |
Whatever you do to one side of the relationship (i.e. quantities to the left of the equals sign or the right) you MUST do to the other side for the relationship to remain valid.
Divide both sides by B gives
| A | x | B | = | R | x | S |
| B | B |
which simplifies to:
| A | = | R | x | S |
| B |
It seems as if the B has gone from the top left to the bottom right, and indeed any transformation like this is allowed PROVIDING that there are no additions or subtractions on either side. i.e.
| A | + | B | = | R | x | S |
In this equation 'B' cannot be taken to the bottom right and cancelled at the same time on the left, as the term produced on the left by dividing both sides by B:
| A | + | B |
| B |
does not equal A.
The result would be:
| A | + | B | = | R | x | S |
| B | B | |||||
|
Example The equation to calculate the relative molecular mass of an ideal gas may be stated as:
Where m = mass in grams, Mr is the relative molecular mass, P is th epressure, T is the absolute temperature, R is the universal gas constant and V is the volume in litres. To rearrange the equation for Mr it must be taken from the bottom right to the top left (by multiplying both sides by Mr):
And then the P and V terms must be taken from the top left to the bottom right (by dividing both sides by P and then by V) Giving:
|
||||||||||||||||||||||||||||||
Decimals, fractions and percentages
Decimals, fractions and percentages are three ways or representing a part of a whole.
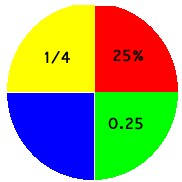 |
The circle is shown divided up into parts. One fourth part may be represented as the decimal 1.5, or the fraction 1/4 or the percentage of the whole 25%. To convert from fraction to decimal the numberat the bottom of the fraction ( the denominator) must be divided into the number at the top (the numerator). Hence, 2/5 is worked as follows: five into 2 doesn't go, add in the next digit (the one after the decimal point). Five into 20 goes 4, therefore the decimal = 0.4 |
Ratios
A ratio shows how one number is related to another. The ratio between two numbers is represented by a colon ':'
value 1 : value 2
|
Example The ratio of 35chlorine atoms to 37chlorine atoms is 3:1 This means that for every four chlorine atoms there are 3 35chlorine atoms for every 1 37chlorine atom (on average). |
A relationship may be given as a ratio, for example, the relationship between the mass of a hydrogen atom and the mass of a helium atom is in a ratio of 1:4.
This tells us that one helium atom has a mass four times that of a hydrogen atom.
Approximations
Approximation is a way of expressing numbers that are almost exact. For example the number 4.99 is approximately equal to 5. As chemistry is an experimental science it is important to realise that measurements are often not exact and that approximations need to be applied.
|
Examples The value of absolute zero is approxiamtely equal to -273 ºC The value of atmospheric pressure in kPa is approximately equal to 100. Avogadro's number is approximately 6.02 x 1023 The mathematical constant 'Pi' is approximately equal to 3.142 |
Most of the accepted values used for the constants of chemistry are available to a higher degree of accuracy than give by the exam boards. They have been approximated for easy usage. For example the value of atmospheric pressure at STP is quoted as 100.0 kPa, when clearly the atmospheric pressure varies from day to day.
In calculations to find the empirical formula of a compound from percentage composition data, the numbers that are obtained are almost never EXACT ratios of number of atoms. However, if they are approximately a simple ratio and we know that atomic ratios have to be integral (whole numbers) then this approximation is good enough.
Proportionality
Proportionality is when the value of one thing is affected in some way by the
value of a second quantity. It is expressed using the proportionality symbol
![]() .
.
|
Example A man's happiness may be proportional to the number of beers drunk.... of course, so could his unhappiness! |
Proportionality is very important in understanding how factors are interlinked. Proportionality may be:
Directly proportional means that there is a straighforward mathematical relationship between two quantities. The mass of a sample is directly proportional to the number of moles of particles present. Direct proportionality is easily expressed as a mathematical relationship:
mass ![]() moles
moles
This means that whatever happens to the mass also happens to the moles. Double the mass and you double the moles etc
Indirect proportionality means that one factor affects the other but not in a direct manner. There may be a logarithmic relationship, a squared relationship or a more complex one.
Inverse proportionality means that an increase in one factor produces a corresponding decrease in another factor. For example an increase in the pressure of a gas causes a decrease in the gas volume. We say that the gas pressure is inversely proportional to the volume.
P ![]() 1/V
1/V
Rate is inversely proportional to the time taken for any given process
Rate ![]() 1/time
1/time
Reciprocals
The reciprocal of any number is 1 divided by that number. The reciprocal of 2 is 1/1.
The reciprocal may be useful when analysing data. For example the Arrhenius equation may be used to find out the activation energy from a series of kinetics experiments:
k = Ae-Ea/RT
Taking natural logs:
lnk = lnA - Ea/RT
If a graph is plotted of k values against the reciprocal temperature values (1/T), a straight line is produced with slope equal to -Ea/R. This allows us to find the activation energy of the reaction.
|
Example The speed of a car and the time taken for a journey have a reciprocal relationship Speed is proportional to the reciprocal of the time taken (also called inverse proportionality) speed |
Significant figures
Pay attention to the number of significant figures required in the answer. “Significant figures” means the number of non-zero digits in a number, counted from the first to the last. The IB usually requires answers to 3 significant figures.
|
Example 1 Write the number 1.04037 to three, four and five significant figures. 1.04037 = 1.04 to three sig figs 1.04037 = 1.040 to four sig figs 1.04037 = 1.0404 to five sig figs (notice the final digit has been rounded up) |
|
Example 2 Write the number 203507 to three, four and five significant figures. 203507 = 204000 to three sig figs 203507 = 203500 to four sig figs (notice the final non-zero digit has been rounded up) 203507 = 203510 to five sig figs (notice the final non-zero digit has been rounded up) |
Decimal places
This means the number of digits after the decimal point. Is should not be confused with significant figures.
Like significant figures, decimal places can be rounded up, or unchanged by consideration of the ‘next’ decimal place. The same rules apply as for significant figure rounding.
Rounding decimals
Calculators present a display with many decimal places. This does not mean that they are extremely accurate, rather that they process the data input precisely. If the original data input had an accuracy of 2 decimal places then the calculator readout can only have this degree of accuracy, no more than that. You should not write down long strings of decimal places in your exam solutions.
|
Example If you have measured a solution volume to an accuracy of ±0.01 cm3 as 20cm3 and then you wish to divide this by 3, the calculator will give you a readout of 6.6666666667 (or something like that depending on the calculator). However, the original accuracy was only 0.01 and so the calculated value should only be written down as 6.67. |
A decimal number can be approximated by rounding up or down by considering the digit AFTER the last digit required.
If this digit is 5 or greater then the previous digit must be rounded up by one. If not then it is left unchanged
|
Example 0.4354 = 0.435 if only three decimal places are required 0.4356 = 0.436 if only three decimal places are required |
Logarithms
Knowledge of logarithms is useful in some areas of the syllabus. A logarithm is the number to which ten has to be raised to obtain a given value.
What does this mean exactly?
A number may be squared and written as follows
42 = 16
The small superscript ‘2’ refers to the fact that the digit 4 is squared. We say that the number 4 has been raised to the power of 1.
This superscript is also called the ‘index’ to which 4 is raised.
When we raise the number 10 to different powers we obtain larger numbers.
If the power is non-integral (i.e. not a whole number) then we can obtain ANY other number.
If we just express a number by the number to which 10 has been raised then this is called the logarithm of that number. (abbreviated to log10 or just log)
|
Example As 102 = 100 then log 100 = 2 As 104 = 10000 then log 10000 = 4 |
What advantage does this have? The advantage of using log forms of numbers is twofold:
|
Example: Calculate the value of the folowing sum using logarithms: 100 x 1000 taking logs log 100 + log 1000
2 + 3 = 5 Therefore log 5 = 100000 |
Natural logarithms
These are logarithms in which the ‘base’ is not 10, rather the natural number ‘e’ which is equal to 1.303
i.e. a natural logarithm is the number to which 1.303 has to be raised to achieve the desired value.
In certain calculations these ‘natural’ logarithms emerge naturally (hence the name). They are abbreviated as 'ln' (loge).
|
Example The natural log of 2, ln2 = 0.693 This means that 1.3030.693 = 2 |
Natural logs appear in some areas of the syllabus, such as the Arrhenius equation for the rate constant relationship with temperature (HL only):
k = Ae–Ea/RT
Taking natural logs throughout:
lnk = lnA – Ea/RT
(notice how terms that were previously multiplied together are now summed in the log form)
This equation now takes the form of a straight line, y = mx + c
Where 'y' is the vertical axis, 'x' in the horizontal axis, 'm' is the slope or gradient and 'c' is the intercept with the 'y' axis.
In this case by rearranging the equation to give
lnk = – Ea/RT + lnA
If a graph is plotted of lnk against 1/T, the gradient is the activation energy Ea and the intercept is 'ln A' (the natural log of the Arrhenius constant). The gradient has a negative slope i.e. it slopes down to the right.
Standard form
Following on from the section on logarithms is should be noted that any value can be produced (to three significant figures) by multiplying a number between 1 and 10 by 10, raised to the power of an integer (whole number)
This is a way of expressing very large or very small values consistently.
|
Example 123000 may be written as 1.23 x 100000 In standard form as 1.23 x 105 |
Notice that dividing by a large number gives a negative index.
This is because:
|
Example 3 0.0045 may be written as 4.5 x 1/1000 (i.e. 4.5 divided by 1000) In standard form 4.5 x 10-3 |
Standard form requires that a number be written as a value between 1 and 10, multiplied by 10 raised to the power of an integer.
The number of decimal places used in standard form usually depends on the precision required. It is often 2 decimal places, for example Avogadro's number 6.02 x 1023
Units and dimensions
Experiments require that values be calculated and measured. Each measurement has two components, the first being the magnitude (the actual number recorded) and the second being the units (the dimensions).
A measurement of distance from the earth to the sun is usually given in km as 400,000,000; This same distance measured in another astronomical unit, the light year, is 4.2 x 10-5 light years. Clearly the two numbers are very different and without the units, or dimensions, they are fiarly meaningless.
Dimensions in the answer to a problem may be found by considering the individual parts of any equation and combining the dimensions of each individual component.
When a solution is made a mass of solute is measured out and dissolved in a volume of water. The mass is measured in grams and the solvent volume in cm3 or dm3. The concentration of the solution is then:
concentration = mass/volume
units of concentration = units of mass / units of volume
units of concentration = g/dm3
If the solution is required in moles/dm3 then the mass must first be converted to moles by dividing by the relative mass of the solute.
When writing the dimensions or units on the same line (i.e. not as a fraction such as g/dm3) the index of any factor at the bottom of the fraction (the denominator) must be changed to the opposite sign, i.e. g/dm3 becomes g dm-3.
|
Example: What are the units of the rate constant in the rate law expression: Rate = k[A]2[B]
Substituting the dimensions into the equation gives: mol dm-3 s-1 = k (mol dm-3)2 x (mol dm-3) Rearranging gives
Now cancel out the similar parts
And bring the parts at the bottom to the top, changing the sign of the index (powers) k = dm6
mol-2 s-1 |
Representing information
You must be familiar with the various different ways to represent information such as graphs and other data forms (pie charts, histograms, bar charts etc.)
Graphs
In chemistry this ALWAYS refers to line graphs. Bar graphs (histograms) are almost never used in chemistry. Bar graphs cannot be used to analyse information further, they only present data for visual comparison.
You must be familiar with the terms intercept, gradient and area as applied to line graphs.
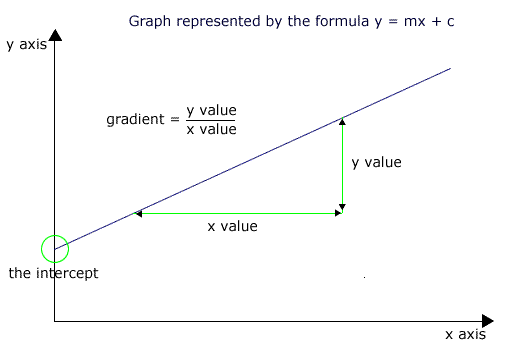
Any graph line can be related to an equation and the simplest is a straight line. All straight lines have the form y = mx + c, where 'y' is the value on the y axis, 'x' is the value on the x axis, 'm' is the gradient and 'c' is the intercept with the y axis (i.e. the y value at the point where the line crosses the y axis).
The gradient (slope) is obtained by measuring the change in y values over a change in x values between two points on the line.
Common mistakes in graphing include axes that are not coherent, i.e. the number of squares that represent a value is different over two parts of the axis line. Students sometimes do this to 'squeeze' the graph into a given size.
Calculators
Be familiar with the display on your calculator. There are several different ways that calculators accept scientific notation input and display it.
Your calculator may display standard form as 1.24 E-10, meaning 1.24 x 10-4 or it could do so without the capital E. On the keypad there may be an "exp" button or it may simply say "E".
Make sure you understand your own calculator!
Methodology
Show each step of the calculation. If an examiner has difficulty reading your answer he can give credit for the method used.
Each step that you have taken should be written down to help you own thought processes. It is far easier to revisit a solution that you have set out correctly for later checking.
Important: If you make an error early in the calculation you may still get credit if you have written evidence that you have used the correct method. This is called 'carrying forward' an error. You will not have the answer correct numerically but the method you have used will demonstrate that you know how to do it.
| 20 |
Next |