|
The rate of a chemical reaction can be determined by measuring the change in concentration of a reactant or product over a period of time. There are many ways that this can be done depending on the nature of the components under study. |
Kinetics experiments
There are a large number of experiments that can be carried out to investigate the rate of a chemical reaction. Analysis of the data can be used to find the orders of reaction with respect to the individual components, determination of the rate constant at a specific temperature and the activation energy. It may even be possible to propose a mechanism.
The following is a list of common experiments:
- The decomposition of hydrogen peroxide using a catalyst.
- The reaction between hydrochloric acid and sodium thiosufate solution.
- The reaction between zinc and sulfuric acid in the presence of a copper ion catalyst.
- The iodine clock reaction (example: potassium iodide and hydrogen peroxide in the presence of sodium thiosulphate and starch indicator).
- The reaction between marble chips and hydrochloric acid solution.
- The hydrolysis of an ester by dilute acid.
- The reaction between a haloalkane and dilute sodium hydroxide solution
The above reactions have some common characteristics:
- 1 They are all reasonably slow reactions
- 2 They all have a component that can be measured
They can be sub-divided into two types:
- 1 Those that are continuously monitored
- 2 Those that measure the time taken to reach a certain point.
The first type allows the rate to be measured at any time by graphing data, while the second type only measures the average rate over a specific time of reaction.
The decomposition of hydrogen peroxide
Hydrogen peroxide decomposes according to the equation:
2H2O2(aq) ![]() 2H2O(l) + O2(g)
2H2O(l) + O2(g)
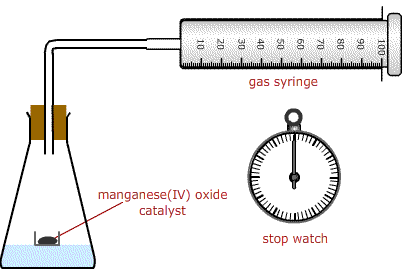
At room temperature the reaction is very slow, but in the presence of a catalyst (usually manganese(IV) oxide) the rate becomes moderate to fast. The progress of the reaction can be followed by measuring the volume of oxygen liberated at regular time intervals.
Hydrogen peroxide is available in 100 vol solution, meaning that 100 volumes of oxygen is produced from 1 volume of hydrogen peroxide.
|
Example: 1000 cm3 of 100 vol hydrogen peroxide releases 100,000 cm3 of oxygen At RTP volume of 1 mole of gas is approximately 24 dm3 100,000 cm3 of oxygen = 100 dm3 = 100/24 mol = 4.17 mol According to the equation: 2H2O2(aq)
1 mol oxygen is produced from 2 mol hydrogen peroxide. Hence, 100 vol hydrogen peroxide has a concentration = 4.17 x 2 = 8.34 mol dm-3 |
Part 1 - determining rate of reaction
Prepare a 10 vol solution of hydrogen peroxide by pipetting a 25ml aliquot of the 100 vol hydrogen peroxide solution into a 250 ml volumetric flask and making up to the mark with distilled (deionised) water. Invert the volumetric flask several times to mix.
 Measure
out about 1 g manganese(IV) oxide catalyst into a small metal cap. Place the
cap carefully on the bottom of a conical flask.
Measure
out about 1 g manganese(IV) oxide catalyst into a small metal cap. Place the
cap carefully on the bottom of a conical flask.
Transfer 25 ml of the hydrogen peroxide solution into the volumetric flask using a pipette, being careful not to disturb the contents of the metal cap. The cap may float on the hydrogen peroxide solution.
Connect a gas syringe to the flask as in the diagram.
Shake to mix the hydrogen peroxide and catalyst and start timing.
Record the volume on the gas syringe every 20 s.
Repeat the procedure using 20 ml hydrogen peroxide solution and 5 ml water; 15 ml hydrogen peroxide/10 ml water; 10 ml hydrogen peroxide/ 15 ml water; 5 ml hydrogen peroxide/20 ml water.
Part 2 - the activation energy
Choose a mixture from part 1 that has a reasonably slow rate.
Repeat the procedure at several different temperatures.
The temperature is controlled by immersing the reaction mixture in a thermostatically controlled water bath and allowing the hydrogen peroxide temperature to stabilise before the reaction. This cn be checked by continuous measurement using a thermometer.
Once again, all qualitative and quantitative data must be recorded, preferably in a table.
Raw data
An example of a possible tabulated set of results is shown below:
| volume of gas evolved / ml ± 1 | |||||
| time/ s | 25 ml H2O2/ 0 ml H2O (± 0.1) | 20 ml H2O2/ 5 ml H2O (± 0.1) | 15 ml H2O2/ 10 ml H2O (± 0.1) | 10 ml H2O2/ 15 ml H2O (± 0.1) | 5 ml H2O2/ 0 20 ml H2O (± 0.1) |
| 0 | |||||
| 20 | |||||
| 40 | |||||
| 60 | |||||
| 80 | |||||
| 100 | |||||
| 120 | |||||
| 150 | |||||
Observations: The hydrogen peroxide effervesced on mixing with the catalyst. The first two reactions showed noticeable heat evolution (exothermic reaction).
The data is then recorded for the reaction at different temperatures using the 15 ml H2O2/ 10 ml H2O mixture.
| volume of gas evolved / ml ± 1 | ||||
| temperature / ºC ± 0.5 | 30.0 | 42.5 | 53.0 | 60.0 |
| time/ s | ||||
| 20 | ||||
| 40 | ||||
| 60 | ||||
| 80 | ||||
| 100 | ||||
| 120 | ||||
| 150 | ||||
Analysing the data
Data analysis - part 1
The data from the first part is plotted graphically with the volume of gas evolved (y - axis) against the time (x- axis). The points are joined using the best fit curve. The tangent to the curve is drawn where the curve passes through the origin.
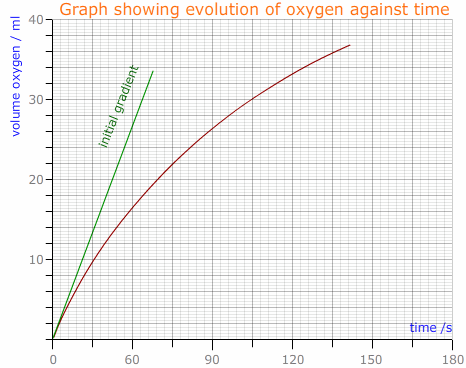
The gradient of the curve provides the initial rate of reaction.
The concentration of hydrogen peroxide is then plotted (x-axis) against the rate of reaction (y-axis) to find the order of reaction with respect to hydrogen peroxide.

From this, the rate constant can be determined.
Rate = k[H2O2]x
Data analysis - part 2
Once the order of reaction is determined the rate constants can be calculated at the different temperatures.
Arrhenius equation gives the relationship between the activation energy and the rate constant at different temperatures (given in the data booklet):
k = Ae-Ea/RT
The loge (natural log, ln) form of the Arrhenius equation is:
ln k = lnA - Ea/RT
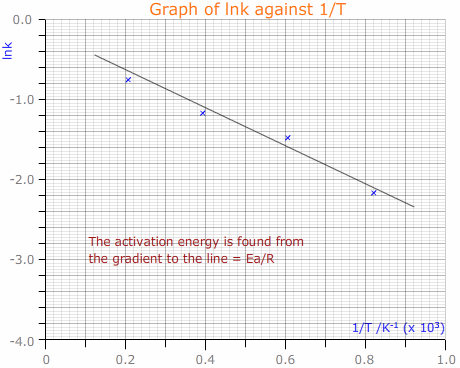
Hence, a plot of ln k against 1/T gives a straight line with gradient - Ea/R
This then allows calculation of the activation energy, Ea.
Treatment of errors and inaccuracies
Clearly this is a long experiment as several runs must be carried out to obtain the order of reaction and then several more at different temperatures to obtain the activation energy. There are many areas where inaccuracies can arise.
Instrumental tolerances can be summed as percentages for each measurement to find the overall instrumental error. For example the gas syringe alone has an inaccuracy of about ± 1. This equates to an average percentage error of about 2%.
However, probably the greatest inaccuracy comes from gauging the slope of the tangent to the curve at t=0.
There are likely to be issues with temperature control in part 2, unless the reaction is carried out under thermostatically controlled conditions, which is not always available in a school.
