|
There are several ways to determine the empirical formula of an unknown compound, but the mass change during reaction due to absorption or loss of a gas affords a simple way of approaching the problem. These experiments determine the empirical formula of two oxides, one by oxide formation and the other by oxide reduction. |
 |
Law of conservation of matter
The basis behind all mass measurement experiments is the law of conservation of matter, which states that matter and hence mass can be neither created nor destroyed.
Hence the total mass before must always equal the total mass after reaction.
When a metal is heated in air any increase in mass must be due to oxygen gas combining with the metals creating a metal oxide. The formula of the oxide can be obtained by mass measurements.
When a metal oxide is reduced to pure metal, the formula of the metal oxide caqn be determined by considering the ratio of mass (and hence moles) of the mass loss (due to oxygen) and the final mass of metal.
The reaction between magnesium and oxygen
Part 1 - the reaction
1 A crucible and lid were carefully weighed on a top pan balance.
2 Some pieces of magnesium ribbon were added to the crucible and it was weighed once more with the lid.
3 The crucible was heated strongly while supported on a pipe-clay triangle
4 The lid of the crucible was periodically raised to ensure that a good stream of air was reaching the magnesium.
5 Once no further change was observed, the apparatus was allowed to cool and the crucible, lid and residue were then weighed.
The procedure was repeated twice more to obtain more reliable results.
Recording the data
All data is recorded, both quantitative and qualitative, with units and inaccuracies.
Raw data
The data is tabulated for easy access.
Table of data showing the masses recorded during the experiment
| Expt | mass crucible & lid /g ± 0.01 | mass crucible & lid + Mg /g ± 0.01 | mass crucible & lid + residue /g ± 0.01 | Observation in residue |
| 1 | 35.20 | 35.95 | 36.38 | white powder with black specks |
| 2 | 36.35 | 37.02 | 37.39 | white powder with black specks |
| 3 | 36.15 | 37.09 | 37.60 | white powder with black specks |
Data analysis
The data analysis may be carried out and presented in a table. The moles column depends on the formula:
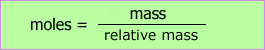
| Expt. | mass crucible & lid + Mg - mass crucible & lid /g ± 0.02 | moles magnesium | mass crucible & lid + residue - mass crucible & lid + Mg /g ± 0.02 | moles oxygen |
| 1 | 0.75 | 0.0309 | 0.43 | 0.0269 |
| 2 | 0.67 | 0.0276 | 0.37 | 0.0231 |
| 3 | 0.94 | 0.0387 | 0.51 | 0.0319 |
Then the appropriate calculations are shown:
Average moles of magnesium = (0.0309+0.0276+0.0387)/3 = 0.0324
Average moles of oxygen = (0.0269+0.0231+0.0319)/3 = 0.0273
Divide through by the smallest number: ratio of magnesium to oxygen = 0.0324/0.0273 : 1
Hence ratio of magnesium atoms to oxygen atoms = 1.19 : 1 (this is close to a 1:1 ratio)
Hence as the number of atoms must be integral, the formula = MgO
Treatment of errors and inaccuracies
These should be recorded as percentage inaccuracy and then propagated through a typical series of steps:
1 Percentage error in mass of magnesium = 100 * 0.02/0.75 = 2.67%
2 Percentage error in mass of oxygen = 100 * 0.02/0.43 = 4.65%
Total percentage error = 7.32%
If this is applied to the ratio of magnesium to oxygen we get: magnesium 1.19 ± 0.09 : 1 oxygen
The reduction of a metal oxide
Metal oxides of weakly reactive metals can be reduced in a stream of hydrogen or methane gas to the pure metal. This allows determination of the empirical formula of the metal oxide by mass measurement before and after.
Experimental procedure
A known mass of a metal oxide is heated in a test tube with a small hole in the closed end to allow for the escape of exhast gases.
The gas is passed over the heated metal oxide until no further change is seen. The exhaust gases are ignited during the reaction to prevent unburnt flammable gas from entering the laboratory.
When the reaction is complete the gas flow is continued until the test tube is cool. This is to prevent the entry of oxygen into the tube which could re-oxidise the hot metal.
Data recording
Mass of empty test-tube before reaction
Mass of test-tube and metal oxide before reaction
Mass of test tube and residue after reaction
Data analysis
Mass of metal oxide = mass of test-tube with metal oxide - mass of empty test-tube
Mass of metal = mass of residue - mass of empty test-tube
Mass of oxygen lost = mass of metal oxide - mass of metal
Find moles of metal and oxygen lost
From mole ratio determine the empirical formula
