|
Spontaneity is a term referring to the thermodynamic possibility of reaction. It is not to be confused with the 'usual' meaning of sudden behaviour. This section looks at how we can use the electrode potentials to predict whether reactions are possible, based only on thermodynamic considerations. |
|
Spontaneity of a reaction
Spontaneous in this context does not mean 'happens immediately'. It just means that the reaction is possible in terms of the energetics (thermodynamics) of the process. Another word that could be used is 'feasible'.

Feasible reactions can be identified from the relative electrode potential values of the reacting species.
Any combination of an oxidising agent with a reducing agent, where the difference in electrode potentials is greater than 0.3 V. Basically something on the left will react with something higher up from the right hand side.
The equations for the reactions can be constructed by first balancing the number of electrons in each half-equation and then adding the half-equations together.
Prediction of spontaneity
Electrode potentials for redox systems can be used to predict whether or not a proposed reaction could proceed. Take the reaction between copper ions and zinc metal. The two half-equations are:
|
Zn2+ + 2e Cu2+ + 2e |
The zinc half-equation is reversed and added to the copper half-equation:
|
Cu2+ + Zn
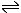 Cu + Zn2+
Cu + Zn2+ |
This is the proposed reaction. By inspection we can see that if the reaction proceeds the copper ions are going to be reduced (they have electrons added) and the zinc atoms are going to be oxidised (they have electrons removed).
The zinc is said to be the oxidised state (the part getting oxidised) and the copper ions the reduced state (the part getting reduced).
To find spontaneity we apply the equation:
|
Eº (species that gets reduced) - Eº (species
that gets oxidised) = Eº (cell potential)
|
- If the E (cell potential) is negative then there is no reaction between these species
- If the value given lies between 0 and 0.3 then an equilibrium is established
- If the value for E (cell) is greater than +0.3 then reaction between these species is spontaneous
As:
Cu2+ + 2e 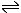 Cu Cu |
Eº = +0.34V | |
| and | ||
Zn2+ + 2e 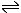 Zn Zn
|
Eº = -0.76V | |
| then | ||
| E = E (red) - E (ox) | E = +0.34 - (-0.76)V | |
| E = + 1.10V |
The answer is positive and greater than 0.3V therefore the reaction is spontaneous - zinc reacts with copper ions.
|
Example: Is the reaction between dichromate ions and tin 2+ ions spontaneous?
Spontaneity is decided by applying E = E (red) - E (ox) In this case the Cr2O72- is reduced and the Sn2+ oxidised therefore E = 1.33 - 0.55 = 0.78 V This is a positive value greater than 0.3 therefore the reaction is spontaneous. |
Feasible reactions can be identified by any combination of an oxidising agent with a reducing agent, where the difference in electrode potentials is greater than 0.3 V. Basically something on the left will react with something higher up from the right hand side.
The equations for the reactions can be constructed by first balancing the number of electrons in each half-equation and then adding the half-equations together.
|
Example: Construct the equation for the reaction between dichromate ions and tin 2+ ions The dichromate half-equation is: 1 Cr2O72-(aq)
+ 14H+(aq) + 6e- And the tin 2+ half-equation is: 2 Sn4+(aq)
+ 2e- By inspection we can see that the dichromate equation needs six electrons on the left hand side whereas the tin 2+ equation has only two electrons on the right hand side. We must, then, multiply the tin 2+ equation by three before adding them.
Whether or not the reaction will be spontaneous is decided by applying E = E (red) - E (ox) In this case the Cr2O72- is reduced and the Sn2+ oxidised therefore E = 1.33 - 0.55 = 0.78 V This is a positive value greater than 0.3 therefore the reaction is spontaneous. |
Exceptions
1 These standard electrode potential values refer to standard conditions i.e. 1.0 Molar concentrations at 25ºC and atmospheric pressure. If these conditions change then so does the electrode potential. In other words, for calculating cell potential, or spontaneity of reaction, it is important to understand that variations occur.
For example, according to standard electrode potentials, manganese IV oxide will not react spontaneously with hydrochloric acid, however this is the standard preparation of chlorine in the laboratory.
| MnO2(s) + 4H+(aq) + 2e- |
Eº = 1.23 V | |
| Cl2(g) + 2e- |
Eº = 1.36 V | |
| Predicting spontaneity, E = E(red) - E(ox) | = 1.23 - 1.36 | E = - 0.13 V |
| Negative value therefore no reaction!! |
In the lab preparation the manganese IV oxide is heated with the concentrated HCl - these are not standard conditions, the temperature is much greater than 25ºC and the concentration of the acid much greater than 1.0 mol dm-3. Under these new conditions the reaction becomes spontaneous and proceeds at a comfortable rate to collect the chlorine gas produced.
|
MnO2(s) + 4H+(aq) + 2Cl-(aq)
|
Gibb's free energy
For any reaction to proceed the Gibb's Free Energy change, ΔGº (a measure of the entropy of the universe) must have a negative value. It follows that as the requirement for spontaneity of a reaction according to electrode potentials is for the value of Eº for a redox reaction to be positive then this must be related to a negative Gibbs Free Energy change.
|
ΔGº = -nEº
|
where 'n' is a proportionality constant.
It turns out that ΔGº depends on the total electrical charge transferred during reaction. This may be given by the number of moles of electrons, z, and the total charge on one mole of electrons transferred during the redox process. Thus:
|
ΔGº = -zFEº
|
Where 'z' is the moles of electrons transferred and 'F' is the charge on one mole of electrons (1 Faraday = 96,500 Coulombs approx).
This equation allows calculation of the Gibb's Free Energy change from a consideration of the electrode potentails of the redox components.
|
Example: Find the Gibb's Free Energy of the reaction between a solution containing copper 2+ ions (1.0 mol dm-3) and a sample of zinc metal at 25ºC.
It should be remembered that this value only applies to standard conditions and that any change in conditions will cause a consequent change in the value of both E and ΔG |
|||||||||||||||||||||||||||||||

 (Eº
= + 1.33 V)
(Eº
= + 1.33 V)