Theory

All salts dissociate 100% in aqueous solution. When one of the ions is derived from a weak acid or a weak base it interacts with the water solvent molecules resulting in a pH value that is not 7. As identified in the previous two sections, salts formed from weak acids and strong bases are basic by hydrolysis and salts formed from strong acids and weak bases are acidic by hydrolysis.

Calculation of the interaction between the ions and the water solvent involves certain assumptions. These are not always valid for very high, or very low concentrations, but suffice under normal experimental conditions.

top

Salts formed from weak acids and strong bases

These are basic by hydrolysis. This is best understood by looking at a specific example, sodium ethanoate.

Sodium ethanoate is the salt of sodium hydroxide (a strong base) and ethanoic acid (a weak acid). Sodium ethanoate is 100% ionic and dissociates completely in solution:

The ethanoate ions interact with (are hydrolysed by) the water solvent and an equilibrium is established:

This hydrolysis equilibrium results in the formation of hydroxide ions in solution. This gives the solution its basic nature. We can assume that the concentration of hydroxide ions is equal to the concentration of ethanoic acid molecules formed. i.e.

We can now write a new expression for the hydrolysis equilibrium with a constant Kh.

However, the ethanoic acid molecules formed are themselves involved in an equilibrium and dissociate forming ethanoate ions and hydrogen ions:

This is the familiar acid dissociation constant expression, Ka:

and if we consider the expression for the dissociation of water, Kw:

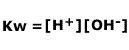
Dividing Kw by Ka gives us the expression for Kh

Hence, in order to find the hydroxide ion concentration for sodium ethanoate we can use Kw/Ka:

As Ka goes on the bottom of the fraction, it is turned upside down and multiplied. The hydrogen concentrations cancel out.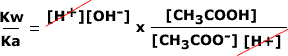
This leaves the ratio of Kw to Ka as follows:
Rearranging the equation by taking the ethanoate ion concentration to the left hand side at the top gives:
and as [CH3COOH] = [OH-]
Then:
So, by taking the square root of the left hand side we can obtain the [OH-] value:

Once the [OH^-] is calculated the pOH can be obtained from pOH = -log[OH^-] and the pH = 14 - pOH

The ethanoate ion concentration can be taken as the original concentration of the sodium ethanoate. This is a fair approximation.

top

Salts formed from strong acids and weak bases

Let's use the most familiar example of ammonium chloride. This is the salt of a weak base (ammonia) and a strong acid (hydrochloric acid).

Ammonium chloride dissociates 100% in solution into ammonium ions and chloride ions. The ammonium ions interacts with the water solvent to produce hydrogen ions and ammonia:

Dissociation of ammonium chloride
Hydrolysis of ammonium ions
We can write an equilibrium for this hydrolysis:
The ammnonia molecues that are formed in the last equilibrium also interact with water molecules forming OH-
This can be written as the Kb equilibrium expression:
Now dividing Kw by Kb gives
Which gives the equation for Kh = Kw/Kb
and as [H+] = [NH3]
We can calculate the hydrogen ion concentration from:

top