|
The pH scale is related to the hydrogen ion concentration via a logarithmic scale. |
|
Using the pH scale
The concept of pH comes from a consideration that acidity is due to the presence of H+ ions in the water. These H+ ions come from the reversible breakdown of the water H2O molecules.
H2O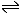 
H+ + OH- |
It may be seen that the breakdown of one molecule of water will produce 1 of each of the resulting ions.
We could therefore measure acidity by simply measuring the concentration of hydrogen ions in the sample. This would, however, lead to very small and inconvenient numbers, as the concentration in pure water at 25ºC is actually 1 x 10-7 moles dm-3
Numbers that are more easily handled are produced by using logarithms (i.e. expressing the number as the power to which 10 has to be raised to achieve the number - this is a common mathematical method)
| log 1 x 10-7 = -7 |
This gives very small numbers a negative value and so a simple change of sign is performed making it positive. Thus the expression for potential hydrogen (pH) is:
| pH = - log [H+] |
Low pH value are acidic, higher values are basic.
|
Example: Calculate the pH of a 0,01 moles dm-3 solution of a strong acid HCl. As the acid only contains one hydrogen atom it will only produce one hydrogen ion per molecule when dissolved in water. Therefore the H+ concentration is = 0.01 moles dm-3 log 0.01 = -2 pH = 2 |
The pH range
At 25ºC the equilibrium H2O 
H+ + OH- gives a value for both the H+ and
OH- ions concentrations as 1 x 10-7 mol dm-3
According to the equilibrium law, Kc (the equilibrium constant) must remain the same, providing the conditions remain constant.
∴ .gif)
|
As the water concentration is very large in comparison to the other concentrations, slight changes in H+ and OH- do not affect it and so we may remove it from the equation, defining a new constant Kw (called the ionic product of water).
Kw is equal to 1 x 10-14 mol2 dm-6 at 25 ºC. Consequently any increase in [H+] must be accompanied by a corresponding decrease in [OH-] to maintain the constant value of Kw.
The pH range becomes 0 to 14 under the usual concentration conditions of the laboratory, where pH 0 represents very strong acid and pH 14 represents strong base.
|
Example: Calculate the pH of a 0.01 moles dm-3 solution of a strong base NaOH As the base only contains one OH group it will only produce one hydroxide ion per molecule when dissolved in water. Therefore the OH- concentration is = 0.01 moles dm-3 As the ionic product of water at 25 ºC [H+] x [OH-] = 1 x 10-14 Then [H+] = 1 x 10-12 log 1 x 10-12 = -12 pH = 12 |
pH scale calculations
Remember that a logarithm is the power to which 10 must be raised to get the given number:
|
number
|
expressed as a power of 10
|
logarithm
|
|---|---|---|
|
1
|
100
|
0
|
|
10
|
101
|
1
|
|
100
|
102
|
2
|
|
1000
|
103
|
3
|
|
10000
|
104
|
4
|
|
0.1
|
10-1
|
-1
|
|
0.01
|
10-2
|
-2
|
|
0.001
|
10-3
|
-3
|
|
0.0001
|
10-4
|
-4
|
Thus a change of 1 in the pH scale represents a change by a factor of 10 in the acidity or basicity of the solution.
|
Example: Hydrochloric acid with a measured pH of 2.3 is ten times as 'strong' as hydrochloric acid with a measured pH of 3.3. The term 'strong' means that there is a concentration of ten times as many hydrogen ions in the solution with a lower pH. |
Summary of pH measurement
- The pH scale measures the degree of acidity
- The scale runs from 0 to 14
- It is a measure of the concentration of hydrogen ions
- As the hydrogen ions increase the pH decreases
- It is a logarithmic scale
- A change of pH by one unit corresponds to a ten times change in hydrogen ion concentration.
