|
Flour mills and coal mines are subject to sudden violent explosions if the amount of dust in the air is not restricted. These are both examples of the increased reactivity of powders when compared to larger pieces of matter. |
Effect of particle size
The word 'particle' may cause confusion here. It is not the size of the molecules (atoms or ions) that is being referred to, but rather the size of lumps of solid (crystals, powder particles, etc) that are mixed with a liquid (or gaseous reagent).
Simple experiments demonstate to us that powders react much faster than lumps of solid. For example, in the reaction between zinc and excess dilute sulfuric acid, the reaction carried out with zinc powder is faster than that carried out using zinc granules.
Zn + H2SO4 ![]() ZnSO4 + H2
ZnSO4 + H2
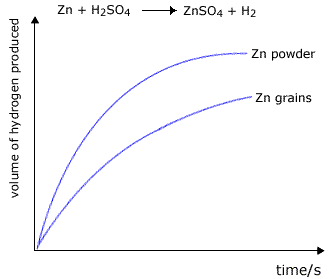 |
The volume of hydrogen produced is greater at any chosen time for the powdered zinc. However, the total final volume of the hydrogen will be the same providing that the mass of zinc used is the same in both experiments (and that there is an excess of sulfuric acid). |
From the collision theory it is easy to appreciate that particles can only collide with other particles at the surface of a solid.
If the particles of one component are aggregated into a larger piece, then the only place that collisions can occur is at the surface. So, it is the total surface available that is important.
In order to understand why changing the particle size affects the rate of a reaction, we can look at the relationship between volume and surface area of shapes.
Volume - surface area relationship
If a large cube is cut into eight identical smaller cubes, how does this affect the overall volume and the overall surface area? This is a very useful practical exercise to carry out.
|
|
From the diagrams, the effect of cutting a cube into 8 smaller pieces has doubled the surface area, while the volume remains the same. We can extrapolate this idea to say that whenever the grain size is decreased the overall surface area to volume ratio increases.
Reactions occur by means of collisions at the surface, so if there is more surface available then there are more collisions and the rate of reaction increases.
Gases
The smallest grouping of particles possible is one particle on its own. In other words, when all of the particles are separated, then the surface available for reaction is at a maximum.
This is the situation in the case of gases. According to our definitions of an ideal gas, gases exist as discrete particles, between which no forces exist. The surface area of a group of discrete particles is the sum of the surfaces of the particles themselves, and is therefore at a maximum in gases. For this reason, gases tend to react rapidly.
Solutions
The solute particles are surrounded by solvent particles in solutions and this slows their reactions down relative to that of gases. However, solutions are able to react much faster than solids.
There are, in fact, very few examples of solids reacting with one another at any appreciable rate.

