IB Chemistry - Energetics

IB Chemistry home > Syllabus 2016 > Energetics > Disorder and spontaneity

Syllabus ref: 15.2

Entropy has been called 'nature's arrow', as all natural systems move towards a state of maximum disorder. This is one of the statements of the second law of thermodynamics. The reasons for this lie in the statistics of natural systems, but for simplicity we can consider entropy to be the degree of disorder within a substance.

Entropy is a state function, i.e. it depends only on the state of the substance and not how that state was reached.

Disorder

Disorder is the natural state of things, just think about your bedroom! Without careful attention a bedroom soon becomes cluttered with things all over the place.

The reason for this is fairly logical; there is only one situation in which everything is ordered in a bedroom, all of the socks in the correct drawer, the bed made, the books on the shelves, tee-shirts folded etc etc. However, there are millions of ways in which the room can be untidy.

If nature is left to itself, the most likely situation is one of disorder - the probability of disorder is much greater.

Natural systems do not usually have someone to arrange them, they adopt the most likely arrangement.

Within a natural system there are billions upon billions of particles, each of which can be given a wide range of energies. The system adopts one of the most likely states, i.e. a disordered state.

top

Entropy

Entropy is the term given to the natural disorder of the universe. If left to itself, the universe tends towards disorder. It can be thought of as an inevitable driving force. Entropy has been called 'nature's arrow'. It is the natural tendency of systems to become disordered.

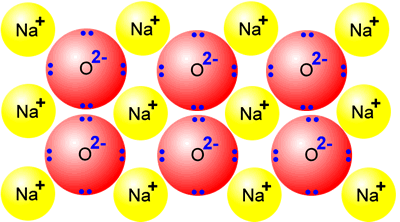If we look at a solid, we can see that all of the particles are carefully arranged in specific locations. This is a highly organised and ordered system. Its entropy is said to be very low.

However, in a gas the particles are free to move randomly and with a range of speeds. The entropy of gases is high.

A liquid has more entropy than a crystalline solid, but much less than a gas.

A solution contains a mixture of solute and solvent particles and has more entropy than a simple liquid but, once again, far less than a gas.

State
Entropy
solid
very low
liquid
low
gas
high

top

Factors affecting entropy

Disorder can be increased by increasing the number of particles that have freedom of movement.

Gas particles have three degrees of freedom:

  1. 1 Translation
  2. 2 Rotation
  3. 3 Vibration

Translation refers to motion in a direction. Rotation is motion about an axis, and vibration means movement of the atoms with respect to one another within particles (stretching and bending of bonds).

Gases then, have a large amount of entropy.

The total entropy depends on the number of possible energy levels that the individual particles can have. This is a function of the temperature.

As the temperature increases the number of energy states available to the particles also increases. The number of possible arrangements of energy over all of the particles increases. This gives the system a greater choice of arrangements, i.e. more entropy.

Hence, entropy is a function of the number of particles and the total energy available to those particles.

The symbol for entropy in chemistry is capital S.

  • Increase number of particles = increased entropy
  • Increase temperature = increased entropy

top

Absolute Entropy

Entropy is defined as the degree of disorder inherent in a system. Unlike the chemical potential energy of a substance, entropy can be measured from an absolute baseline.

When a system has no disorder, i.e. it is perfectly arranged, and it has no energy, (absolute zero kelvin) it can have no entropy.

These conditions are met in a perfect crystallline substance at absolute zero.

This allows us to measure, or calculate, absolute entropy values, i.e. the entropy when compared to this absolute zero entropy baseline.

There are various calculations that make this possible, based on thermodynamic data as well as statistics.

Explanations of these go beyond the scope of this book.

Tables of absolute entropy values are available and may be used to calculate entropy changes from one situation to another. Absolute entropy is measured in J K-1.

Note You should be aware of two important facts:

  1. 1 Gases have much more entropy than solids or liquids.
  2. 2 Entropy increases as the mass and complexity of a molecule increases.

top

Entropy change

The difference in entropy in any process, chemical or physical, is the entropy of the final situation minus the entropy of the initial situation. For a chemical reaction this is the difference between the products entropy and the reactants entropy, called the entropy change. IThe entropy change is symbolised by ΔS, delta S. When the entropy increases, ΔS is positive.

ΔS = S(final) - S(initial)

When the entropy is determined under standard conditions it is called the standard entropy, ΔS.

Example: Does the entropy of the system increase or decrease when a kettle boils?

Before boiling the water is a liquid and has low entropy. After boiling the water becomes a gas and has much higher entropy. Therefore the entropy has increased and ΔS is positive.

Example: Does the entropy of the following reaction increase or decrease ?

N2(g) + 3H2(g) 2NH3(g)

On the left hand side of the equation there are four moles of gas and on the right hand side of the equation there are two moles of gas. The total amount of gas particles is decreasing and therefore the entropy is decreasing, ΔS is negative.

One point to note is that the effect of energy input (temperature increase) on entropy is not the same at all temperatures, but rather depends on the absolute temperature. There is a greater increase in entropy at lower temperatures for a given energy input.

Hence, the entropy change is dependent on the temperature at which the change takes place. This can be expressed by the equation:

ΔS = q/T

where 'q' is the energy input.

top

previous     2024     next