|
Ionic substances exist in giant structures of repeating ions all held together by electrostatic forces. |
|
Electrostatic force between ions
Although not a bond in the classical covalent sense of the word, electrostatic forces hold oppositely charges ions together in an ionic crystal lattice. This force is dependent on the magnitude of the charges on the ions and inversely proportional to the distance between them.
|
|
Where: z1 is the magnitude of the positive ion, z2 is the magnitude of the charge on the negative ion and 'r' is the distance between them.
Consequently, ions with greater charges are held together more tightly and smaller ions form more effective bonds than larger ions. The following examples should make the effect of changing both ionic charge and ionic radius clear.
|
Example: The force of attraction between sodium and chloride ions: This is dependent on the magnitude of the ionic charges. Sodium ions
have a 1+ charge and chloride ions have a 1- charge.
Therefore the distance between is 0.098 + 0.181 = 0.279nm The force of attraction is proportional to 1 x 1 /(0.279)2 = 12.8 This number is meaningless in isolation, but could be used to compare the force of attraction between other ions in an ionic lattice. You will not be asked to do this in an exam |
The previous example considered the force between two singly charged ions. For comparison we can look at the force of electrostatic attraction between two singly charged ions of different radii, such as caesium iodide.
|
Example: The force of attraction between caesium and iodide ions: This is dependent on the magnitude of the ionic charges. Caesium ions have a 1+ charge and iodide ions have a 1- charge. The distance between them is the sum of the ionic radii of the two ions.
Therefore the distance between is 0.169 + 0.219 = 0.388nm The force of attraction is proportional to 1 x 1 /(0.388)2 = 6.6 We can see that this value, proportional to the electrostatic force of attraction, is about one half that of sodium chloride. The 'bond' is weaker. |
A similar comparison could examine the effect of changing the magnitude of charge on the ions, for example in the force of attraction between magnesium and oxide ions in magnesium oxide.
|
Example: The force of attraction between magnesium and oxide ions: Magnesium ions have a 2+ charge and oxide ions have a 2- charge. The distance between them is the sum of the ionic radii of the two ions.
Therefore the distance between is 0.065 + 0.140 = 0.205nm Thus, the force of attraction is proportional to 2 x 2 /(0.205)2 = 95.2 This value is far bigger than that of sodium chloride, a factor of seven times. The force of attraction between magnesium and oxide ions is considerably larger than that of sodium chloride. |
Forces within the lattice
An ionic lattice is the giant framework of repeating positive and negative ions in three dimensions. In the section above we looked at the forces that exist between two oppositely charged ions.
In an ionic lattice each positive ion is surrounded by negative ions and so feels a force of attraction towards all of them. The same case applied to each negative ion, it is surrounded by positive ions and feels the forces of attraction towards all of these neighbours.
|
|
|
|
Sodium ion surrounded by chloride ions
|
Chloride ion surrounded by sodium ions
|
The whole crystal lattice consists of billions upon billions of these ions, each positive surrounded by negative ions and each negative surrounded by positive ions. The forces of attraction pull all of the ions into the best arrangement possible in which all of the forces are at a maximum. This gives us the final crystal lattice structure:
The lattice enthalpy
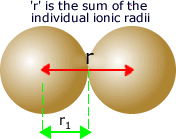 The
distance between them is considered to be the sum of the ionic radii
of the two ions.
The
distance between them is considered to be the sum of the ionic radii
of the two ions. 