|
In chemical processes the ratio of reacting particles is always fixed for a specific reaction. Once the number of particles of any component of a known reaction is determined, it is possible to find the number of particles involved of any other component by using the stoichoimetry of the equation. |

|
The stoichiometry is shown by the relative coefficients of the components appearing in the chemical reaction.
|
Example
4NH3 + 5O2
The stoichoimetry of the reaction tells us that 4 molecules of ammonia react with 5 molecules of oxygen and produce 4 molecules of nitrogen monoxide and 6 molecules of water |
1 mole is equivalent to 6.02 x 1023 molecules therefore the stoichiometry also gives us the ratio of moles reacting.
Consider the reaction:
The stoichiometry of the equation shows us that one atom of iron is needed to react with each atom of sulfur. Extending this idea we can see that the same number of iron and sulfur atoms are always needed for a complete reaction.
Therefore the moles of iron are always equal to the moles of sulfur in this reaction.
If we are told the mass of iron that we start with is 5.6g then we can calculate the mass of sulfur needed. The calculation proceeds via the number of moles. [Relative atomic mass of Fe=56, S=32]
Moles of iron = mass /RAM = 5.6/56 = 0.1 moles
Therefore moles of sulfur = 0.1 moles
RAM of sulfur = 32
Therefore mass of sulfur needed = moles x RAM = 0.1 x 32 = 3.2g
The procedure followed is:
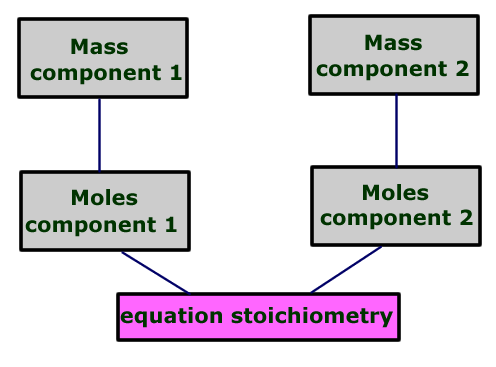
|
Example: Calculate the mass of chlorine needed to completely react with 2.24g of iron [relative atomic masses Fe=56, Cl=35.5]
Mass of iron = 2.24g, therefore moles of iron = 2.24/56 = 0.04 moles from the equation stoichiometry it can be seen that 2 moles of iron react with 3 moles of chlorine therefore 0.04 moles iron react with 0.04 x 3/2 moles chlorine molecules = 0.06 moles realtive molecular mass of Cl2 = 2 x 35.5 = 71 therefore 0.06 moles of chlorine = 0.06 x 71 = 4.26g |

